Retour au sommaire

  ANIMATION  

 

 

    PREAMBULE SOMMAIRE AFFICHAGE    

 

Les méthodes d'animation décrites ici sont basées sur un processus itératif, c'est à dire que chaque position courante, est déduite de la position précédente. L'intérêt de cette technique est qu'elle est très simple à mettre en oeuvre. Son principal inconvénient est que sa vitesse de défilement dépend directement des capacités du système. En effet, comme l'animation n'est pas jouée en fonction du temps, cette dernière se déroule aussi rapidement que le permettent le programme et l'ordinateur qui l'exécute. Il est possible néanmoins de modérer cette vitesse en ralentissant le mouvement des sprites comme cela peut se faire dans =FOOT= à l'aide de sa boîte de dialogue de paramétrages.

Voici donc quelques algorithmes permettant d'orienter et de déplacer des sprites dans un espace de jeu.

 

  1) Orientation:  

Le vecteur s'impose tout naturellement comme l'outil idéal pour définir l'orientation de nos objets mobiles car de surcroît, il peut également nous renseigner sur leur vitesse de déplacement grâce à sa norme.

 

Pour éviter toute confusion dans la suite du texte, je m'en tiendrai au terme de "vecteur directeur" bien que ce dernier d'écrive également la vitesse.

 

  2) Déplacement rectiligne constant:  

Une fois qu'une direction est définie par un vecteur, il devient aisé de déplacer le sprite dans cette même direction. Il suffit pour cela d'ajouter les coordonnées du vecteur directeur, à chaque tour de boucle du jeu, aux coordonnées de la position courante du sprite.

Pour forcer l'objet à se déplacer toujours à vitesse constante, on prendra soin de normaliser son vecteur directeur, à chaque changement d'orientation.

Bien que la trajectoire décrite soit rectiligne entre deux images consécutives, elle peut parfaitement devenir curviligne sur une période plus longue lorsque la direction du sprite change simultanément au cours de son déplacement (cf. l'attaquant suivant le pointeur de la souris dans =FOOT=).

 

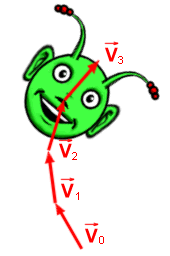sprite en train de changer de direction au cours de son déplacement.

 

 

  3) Déplacement rectiligne uniformément accéléré:  

A présent que nous savons déplacer un sprite dans n'importe quelle direction à vitesse constante, il serait bon de lui ajouter une touche de réalisme. Nous allons pour cela considérer la force d'inertie. Cela se traduira par une accélération uniforme au démarrage de l'objet animé et ce, jusqu'à ce qu'il atteigne sa vitesse maximale.

Pour réaliser cet effet nous avons besoin d'appliquer un coefficient multiplicateur au vecteur directeur. Initialisé à zéro au démarrage du sprite, il sera ensuite incrémenté à chaque tour de boucle de jeu, jusqu'à un seuil limite. pendant toute la durée de l'animation, les coordonnées du vecteur directeur seront multipliées par ce coefficient de plus en plus grand ce qui aura pour effet d'augmenter sa norme, et donc la vitesse du sprite.

 

sprite en train d'accélérer

 

Le raisonnement inverse peut être envisagé pour simuler un ralentissement, à l'instar du ballon terminant progressivement sa course après un shoot.

 

 

  4) Simulation de la gravité:  

Nous avons vu lors de l'article précédent, comment accélérer ou décélérer un objet mobile par un simple calcul itératif. Nous pouvons appliquer ce même principe pour simuler la gravité. En effet, cette dernière peut être considérée comme une force verticale qui s'exerce du haut vers le bas sur les objets concernés. Ainsi, à chaque tour de boucle de jeu, un vecteur G à la composante Y négative et à la composante X nulle, est ajouté au vecteur directeur du sprite à faire chuter. 

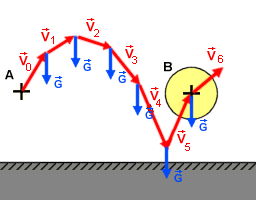Sur ce schéma on peut constater que: V1 = V0 +  G, V2 = V1 + G,...

Soit: Vn = Vn-1 + G

 

Cependant, il faut noter que pendant toute la durée où l'objet est soumit à la gravité, le coefficient multiplicateur n'est plus appliqué à son vecteur directeur de même que ce dernier n'est plus normalisé. En effet, c'est le vecteur G qui modifie, par son ajout,  la norme du vecteur directeur du sprite et donc sa vitesse verticale.

Comme les objets animés ne peuvent se déplacer indéfiniment sans sortir de la zone de jeu, il va falloir à un moment ou un autre gérer leur éventuelle collision avec le sol et les murs qui les entourent...

 

 

  5) Détection des collisions:  

La détection des collisions dans =FOOT= est relativement succincte, et par conséquent assez simple à appréhender. Ceci pour deux raisons essentielles:

Dans ces conditions la détermination d'éventuelles collisions se résume simplement à savoir si le rectangle englobant d'un sprite se trouve ou non à l'intérieur du terrain.

 

Lorsqu'un objet sort du terrain deux réactions sont alors possibles:

 

 

  5) Réaction aux collisions:  

Deux cas sont à distinguer lorsque le ballon percute l'un des côtés du terrain:

1 - Le ballon est à l'intérieur du mur:

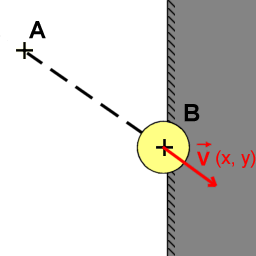Au moment de détecter la collision, le ballon se trouve entre le terrain et le mur: On le décale alors suffisamment pour qu'il soit juxtaposé tout contre la paroi et on inverse la composante X (dans le cas d'un mur vertical) de son vecteur directeur afin qu'il rebondisse.

 

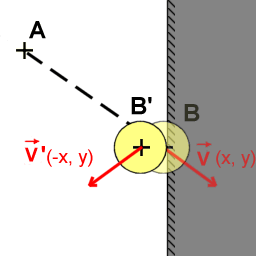
2 - Le ballon à complètement traversé le mur:

Au moment de détecter la collision, le ballon se trouve à l'intérieur du mur: On le décale alors en prenant comme axe de symétrie le mur percuté. On inverse également la composante X (dans le cas d'un mur vertical) de son vecteur directeur afin qu'il rebondisse.

 

La détection des collisions avec réactions est un processus récursif. En effet, dans un quantum de temps, le ballon est susceptible de percuter plusieurs murs, comme le montre l'illustration ci-dessous. Il faut donc procéder aux tests jusqu'à ce que le ballon ne touche plus rien.

 

 

Voilà, tout ou presque à été dit concernant l'animation telle qu'elle est traitée dans =FOOT=. Vous trouverez de plus amples informations en consultant ses sources, notamment les module Animation.bas et ZSprite.cls.

 

 

 

    PREAMBULE SOMMAIRE AFFICHAGE